问题来源:https://www.zhihu.com/question/462218901
原问题:
作为一个未入门的研究生小白,一方面为深度学习的实际效果和应用价值而感到兴奋,另一方面也会担忧自己的个人能力的发展。
个人目前浅薄的看法是,调模型的强应用向的研究工作,由于深度学习目前的黑箱性,对于个人似乎只能积累应用经验,但在数理工具,开发能力等等方面的训练和提升似乎不强。
所以希望自己在调模型以外,打开视野看看一些更有见地的工作。
总之,到目前为止,深度学习领域的发展趋势是什么?有哪些值得关注的新动向?在应用领域,诸如cv,nlp等,研究思路是否有新的变化?
# 回答一
作者:刘斯坦
来源链接:https://www.zhihu.com/question/462218901/answer/1925000483
目录
-
随机初始模型到最终模型之间的插值情况
-
最终模型之间的插值情况
-
神经网络损失面的全貌
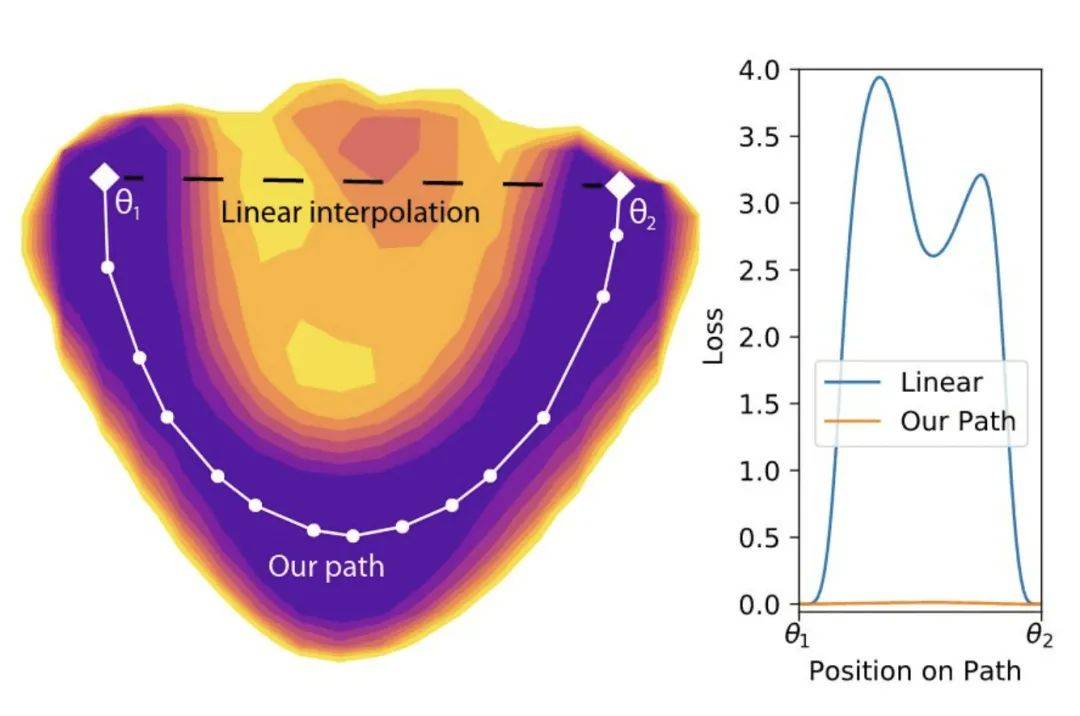
不知道算不算硬核,不过我觉得关于Loss Landscape的研究很值得关注,对理解神经网络的一些特性很有帮助。相关的研究很多,每一个研究都研究了损失面的一个或若干个特性,把他们拢在一起,会发现神经网络的损失面会变得很清晰。
首先有几个基本概念普及一下,一个是所谓“flat wide minima”,极小值所在的损失面越平坦,越宽,泛化性能越好,所以优化的最终目标就是追求flat wide minima。
还有一个就是所谓的线性插值,就是说两个模型,一样的网络结构,不同的参数,对这两个权重进行粗暴的线性加权平均,得到一个新的模型,这个操作就叫线性插值。
通过对模型进行线性插值来观察损失的变化,可以了解损失面的几何结构,这是一个经常使用的工具。
随机初始模型到最终模型之间的插值情况
可以想象一下,一个神经网络经过几十上百个epoch的训练,从随机的初始状态一直到最后的最小值,中间大约会经过各种跌宕起伏。如果粗暴地从随机初始状态到最终状态之间拉一根直线,对模型进行线性插值,然后这条插值的直线投射到损失面上,就得到了插值过程中的损失变化曲线,如果损失面起伏很复杂的话,那这条从直线投射而来的曲线应该也是上下起伏的吧?然后根据Goodfellow在2014年的发现,很多时候这个曲线是单调递减的:
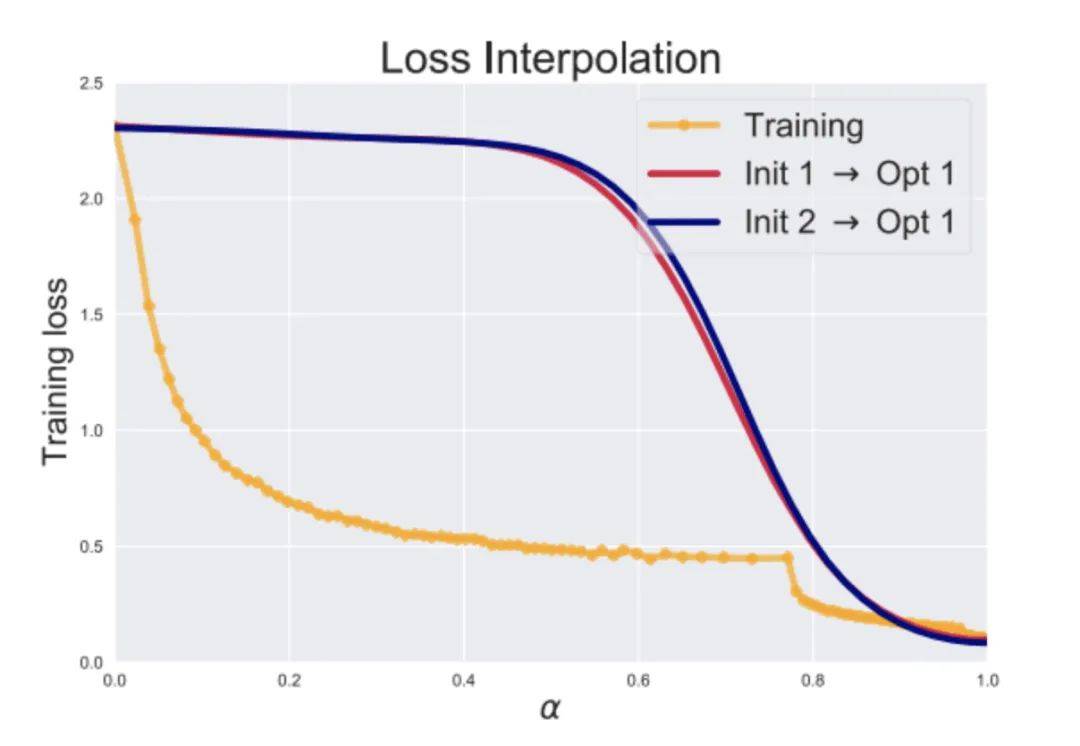
黄线是训练时候跟着梯度在损失面上走出来的损失曲线,蓝线和红线是从不同的初始点到最终模型拉一根直线投射到损失面上的损失曲线。可以看到,这条损失曲线是单调递减的。
这篇文章 Analyzing Monotonic Linear Interpolation in Neural Network Loss Landscapes(https://arxiv.org/abs/2104.11044) 管这个特性叫“单调线性插值”。
文章发现从不同的初始值可以走到同一个模型,殊路同归,而且模型符合单调线性插值,如左图。而这个情况文章 Linear Mode Connectivity and the Lottery Ticket Hypothesis(https://arxiv.org/abs/1912.05671) 也说了,随机初始化位置不同,模型经常就会掉到同一个局部极小值,而这个趋势在训练很早期就已经确定了。
有时候不同的初始值会走到不同的模型,这种情况如果你从init1到opt2拉一根直线去投射,就不是单调的了,也很好理解,因为要翻过一个小山坡,这个情况是右图:
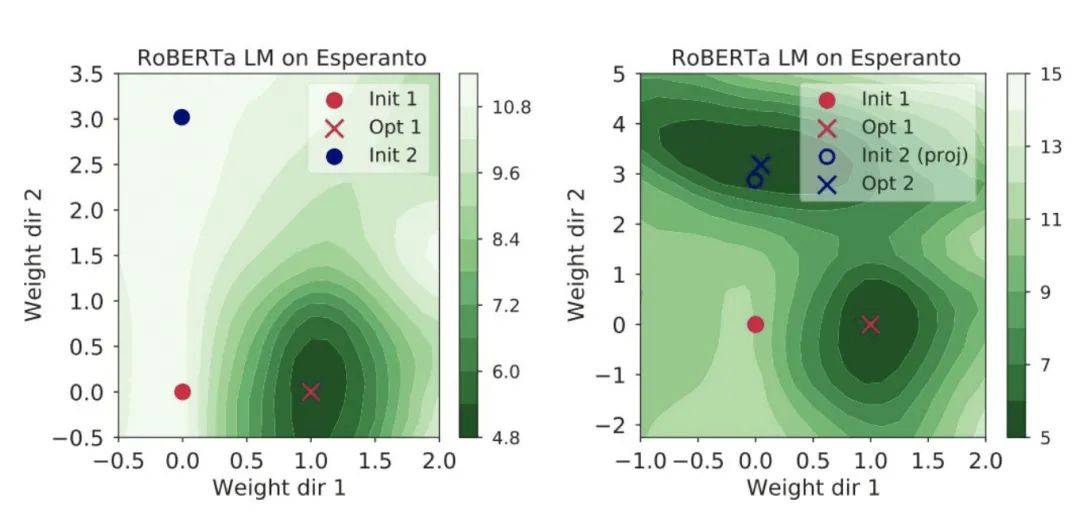
作者发现,如果初始值和终值权重之间的距离越远,单调线性插值就越难。而导致这种情况的因素有:使用大的训练步长,使用Adam优化器和使用Batch Norm。比如使用Adam,经常就会遇到小山峰:
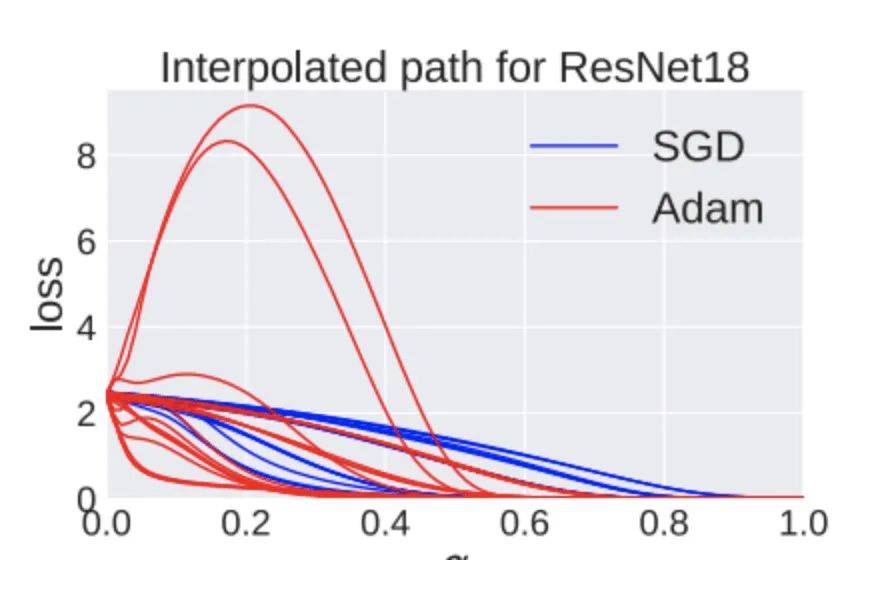
这意味着大的步长和Adam优化器都会促使模型越过山峰。
最终模型之间的插值情况
也有一些论文研究最终模型之间的插值情况,上文说了,从两个初始值出发到达两个极小值,之间可能会有山坡,所以如果对这两个极小值之间进行插值,会投射出这样一条损失线:
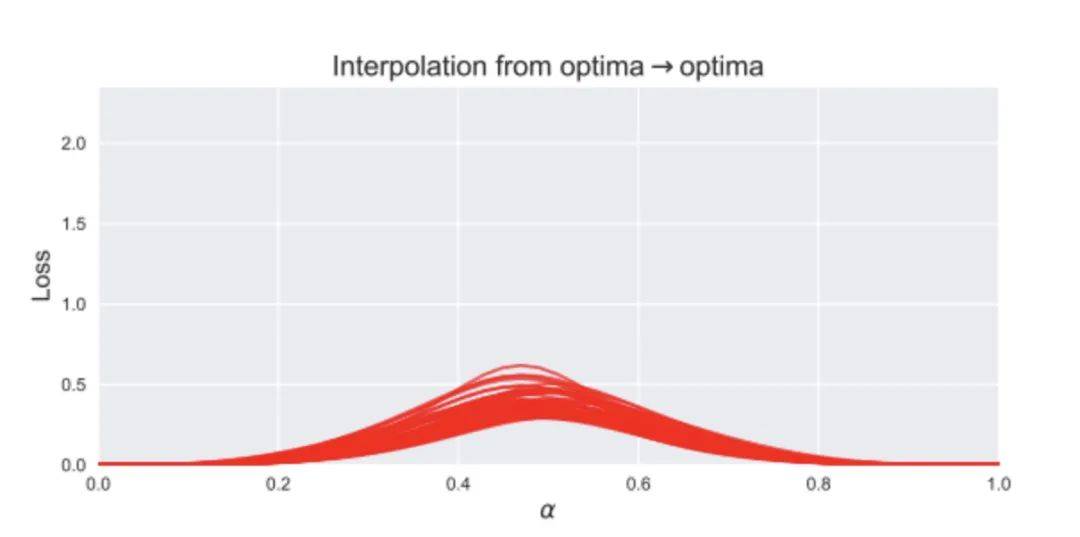
这很好理解,但这却不是真相的全部。
文章 Essentially No Barriers in Neural Network Energy Landscape(https://arxiv.org/abs/1803.00885) 发现,这些极小值之间是可以通过一段一段的直线连接起来的:
如果你直接走直线,就是越过山坡,会跌宕起伏,但如果使用文章中的优化方法,绕着走,肯定可以到达另一个极小值。也就是说,局部极小值之间都可以通过线段连接起来,而且一路上损失都很低(上图右边那条黄线,沿着山谷走,损失一直很低,一直都保持极小值状态)。
而文章 On Connected Sublevel Sets in Deep Learning(https://arxiv.org/abs/1901.07417)则证明,如果使用分段线性激活函数,比如ReLu,那么这个神经网络模型的所有局部极小值其实都是连在一块儿的,他们其实都属于同一个全局最小值。
文章 Landscape Connectivity and Dropout Stability of SGD Solutions for Over-parameterized Neural Networks(https://arxiv.org/abs/1912.10095)告诉我们,神经网络参数量越大,局部极小值之间的连接性越强。
神经网络损失面的全貌
那么综合以上各种论文的结论,基本可以描绘出神经网络损失面的全貌,应该长这样:
极小值都处于同一个高度,属于同一个全局最小值,而且互相之间是连在一起的。那么很容易想到了,如果你往这个沙盘随机扔弹子,是不是更容易掉到那种特别宽的flat minima?没错,文章 The large learning rate phase of deep learning:the catapult mechanism(https://arxiv.org/abs/2003.02218) 发现,使用大的学习率更容易掉到平坦的极小值(flat wide minima),也就是说,学习率一大,相当于在这些山之间乱跳,当然更容易掉到flat wide minima咯。
大胆猜测,根据Lottery Ticket假设那篇论文描述的现象,这里面每一个小山都是一个sub-network
另外还有很多研究表现resnet和mish激活函数可以让损失面更平滑,而Relu会让极小值变得很尖很崎岖。
# 回答二
作者:电光幻影炼金术
来源链接:https://www.zhihu.com/question/462218901/answer/1966379644
提一点浅见:深度学习不能不调参,也不能只调参。
如果不调参,很难大幅超过baseline,尤其是在模型/任务大幅度改变的情况下,所需要的超参数往往截然不同。这样的结果是incremental contribution/lack of novelty,还会引发一系列关于方法的concern。我老板曾经曰过,其实很多reviewer对实验的质疑,都是参数没调好导致的。
如果只调参数,那么格局就有点小了。

想要格局变大,论文中需要有 (1)清晰的motivation(2)干净的逻辑链辅助推理(3)丰富的消融实验(4)好的可视化结果(5)有泛化潜力的结论或者insight。 最好文章能揭示更多未解决的问题。

我们可以欣赏一下swin transformer是怎么做的。
首先swin transformer明确提出了transformer特有的一系列问题,并且有比较充足的逻辑链提出一系列的模块(因为多尺度所以需要分window,因为分开的window不包含边界信息所以要加入shift window)。其次swin transformer做的数据集也足够多,证明其提出的模块可能是广泛有效的。
-------------------
END
--------------------
来源: 计算机视觉联盟
