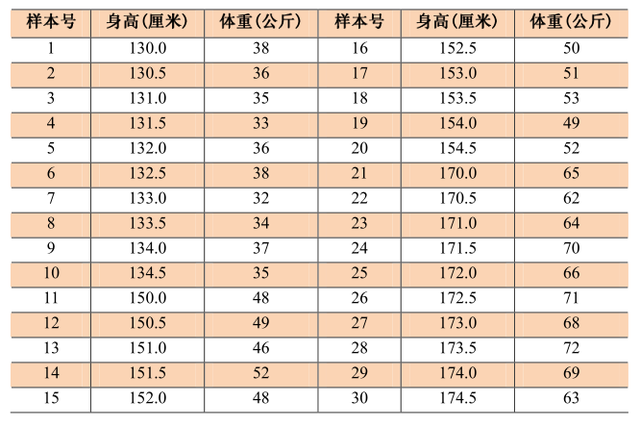
 某学校初中男生身高-体重数据
某学校初中男生身高-体重数据聚类任务: 将上表的样本聚为三类。
分析:任务中没有给出每个类别的标准特征,需要考察样本间的相似情况,将相似的样本聚为一类,此外还要找到每类的标准特征,即聚类中心。
样本的相似性度量
比较两个样本的相似性可转化为测量两个样本点在样本空间的距离,并以此距离的大小作为两样本相似性的度量。
虽然从二维和三维样本空间的图中可以十分清晰地看出样本间的距离远近,从而可以通过目测发现隐藏在二维或三维样本空间中的聚类,但是随着样本空间维数的增加,我们很难再通过目测来进行观察。一般来说,需要用某种合适的聚类算法来解决具体问题。
最简单的聚类算法——胜者为王(Winner Take All)
胜者为王聚类算法采用了一种简单的竞争学习策略。该算法可分为3个步骤:
⑴ 初始化聚类中心
拟将样本聚为多少类,就需要设置多少个权向量,每个权向量代表某一类的聚类中心。本任务要求将30个样本为3类,所以需要3个权向量作聚类中心。
对聚类中心进行初始化的方法很多。例如,可随机指定3个样本作聚类中心,也可以用随机数为每个向量赋值。从表中看出,30个样本的身高特征为130~174.5厘米,可从中随机选3个数135、145、155作为3个权向量的身高特征;身高特征为25~60公斤,可从中随机选3个数40、50、60作为3个权向量的体重特征。如图4-12所示,3个初始权向量分别为:(135,40)、(145,50)、(155,60)。
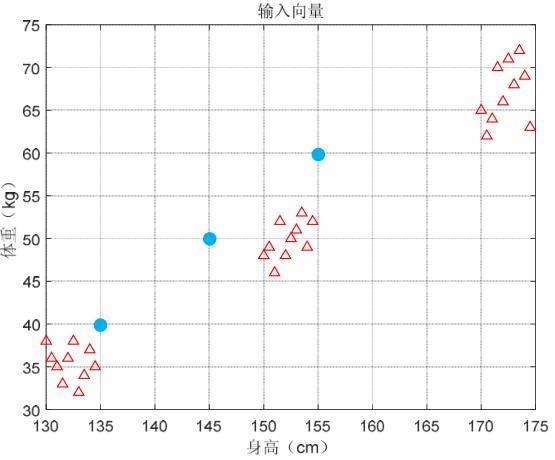 三个初权向量在样本空间的分布图片描述
三个初权向量在样本空间的分布图片描述⑵ 确定竞争获胜的权向量
以前面表中给出的30个样本为训练样本,随机但不重复地从训练集中抽取一个样本作为算法的输入。
每个输入样本均与3个权向量进行相似性比较,即测量当前输入样本在样本空间的位置与3个权向量在样本空间位置之间的距离,这种距离称为欧式距离。与当前输入样本欧式距离最短的权向量在相似性竞争中获胜。
根据几何知识我们知道,若平面上两点A和B的坐标分别为(xa,ya)、(xb,yb),则两点间的距离为
下图标出某个当前输入样本与3个权向量之间的距离和获胜权向量。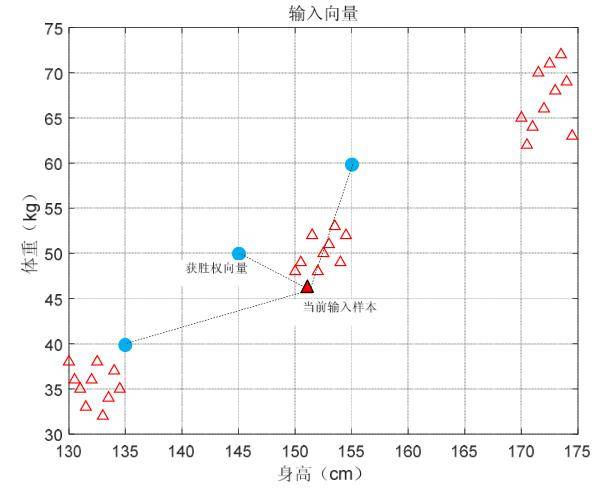
⑶获胜的权向量调整权值
胜者为王竞争学习算法规定,只有才有权进行调整,其他权向量“原地不动”。获胜权向量调整办法是:令获胜权向量向当前输入样本方向移动一步,移动的步长与两点间的距离成正比。比例系数α称为学习率,是(0,1]区间的常数。设α=0.5,获胜权向量调整情况如下图所示,可以看出获胜权向量调整的结果是缩短与当前输入样本的距离。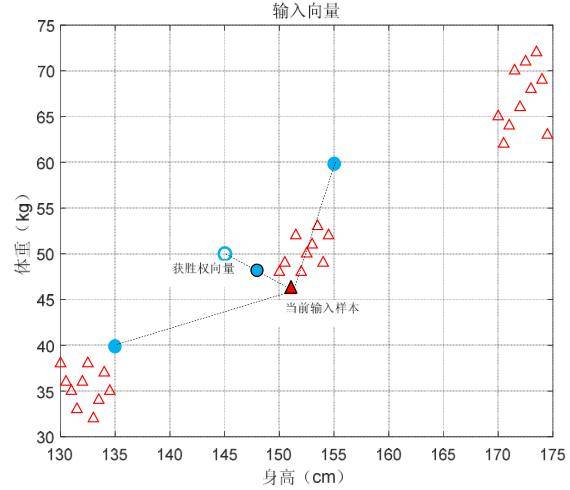
⑷返回步骤⑵输入下一个样本,直到事先规定的训练次数。
来源: 人工智能科普驿站
